Overview
以下的每个排序的写法格式基本按照先介绍基本思想,再描述具体过程,最后是具体代码。关于复杂度等问题后续更新。如有写的不严谨的地方,欢迎指出,相互交流。
###希尔排序
基本思想:将一组数据按照一定的步长分组,进行直接插入排序,然后再缩小步长,再排序,直到步长为1,再进行一次排序,就得到了有序序列。
以下面一组数据为例:
{ 8, 19, 2, 5, 7, 10, 12, 16, 18, 20 }
根据wiki百科,我选择了一种选取步长的方式,即初始取n/2(n为数据的长度)作为步长,其后将步长减半,直至步长减为1.其他步长选取方法可以参见wiki百科。
具体过程:
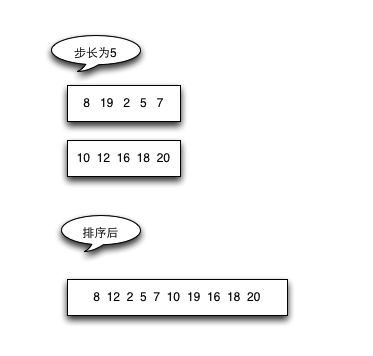
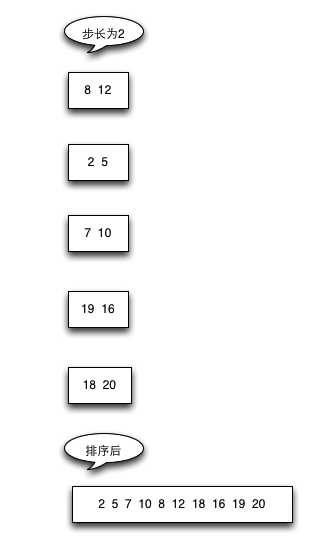
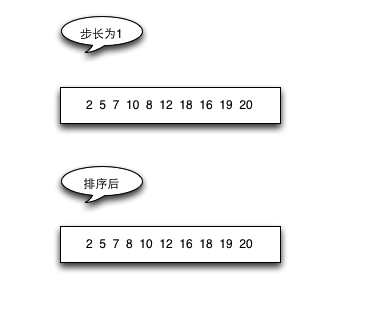
具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
* 希尔排序
*
* 步长选择size/2为并且对步长取半直到步长达到 1
*
* @param d
* 要排序的数组
*/
public static void shellSort(int[] d) {
int size = d.length;
int tmp;
for (int i = size / 2; i > 0; i /= 2) {
for (int j = i; j < size; j++) {
int k = j;
Boolean flag = false;
while (k - i >= 0) {// 有优化的空间,如果两个数比较后没有进行交换,应可以直接跳出循环
if (d[k] < d[k - i]) {
tmp = d[k];
d[k] = d[k - i];
d[k - i] = tmp;
flag = true;
}
if (flag)
break;
k -= i;
}
}
}
}
###堆排序
首先需要知道的知识,二叉树,已知父节点i,左孩子节点(2 * i + 1),右孩子节点(2 * i + 2);若已知孩子节点,父节点为((i - 1) / 2)。
最小堆性质是,父节点的值的大小要求小于等于左右孩子节点的值。
建立最小堆,得到的是递减序列;反之,建立最大堆,得到递增序列。
基本思想:建立一个最小堆(或最大堆,本文中均以最小堆为例)。根据最小堆性质可以知道,根节点元素是最小的元素,因此每次删除这个节点,进行最小堆的调整,一直重复这个过程,直至仅剩最后一个元素,排序完成。
以下面一组数据为例:
{ 8, 9, 2, 5, 7, 10, 12, 16, 18, 20 }
基本过程:
建立最小堆
根据图片指示的顺序,一个一个个将数组中的元素加入到堆中,并进行调整,最终得到最小堆。
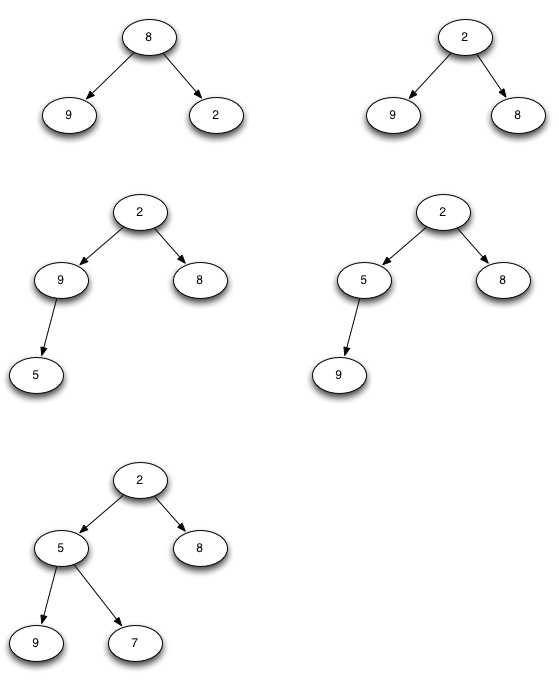
至此省略几步,将数据一个个加入即可。最终得到的最小堆:
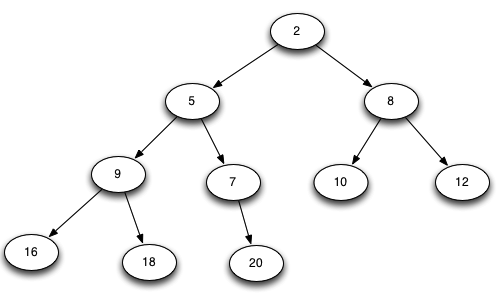
建完最小堆之后,可以清楚看见最小堆的性质,根节点的值一定小于等于左右孩子节点的值。接下来,要做的是将根节点删除,然后将最后一个元素的值赋给根节点,然后进行一个调整。这个过程的图就不一一画了,仅画第一步,接下来的操作类似。
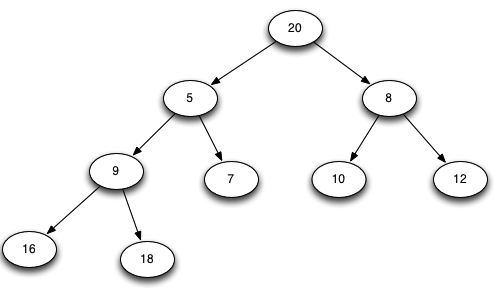
得到一个新的最小堆:
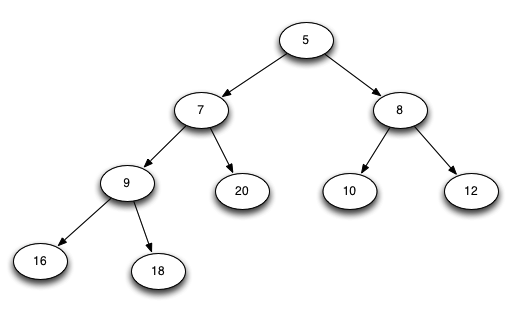
具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/**
* 堆排序
*
* 因为使用的是最小堆,所以得到的序列是递减序列;如果要递增序列则需要使用最大堆
*
* @param d
* 要排序的数组
* @param n
* 数组的长度
*/
public static void heapSort(int[] d, int n) {
int tmp;
for (int i = n - 1; i > 0; i--) {
tmp = d[i];
d[i] = d[0];
d[0] = tmp;
heapMakeDown(d, 0, i);
}
}
/**
* 建立最小堆
*
* @param d
* 要建堆的数组
* @param n
* 数组的长度
*/
public static void makeMinHeap(int[] d, int n) {
for (int i = n / 2 - 1; i >= 0; i--) {
heapMakeDown(d, i, n);
}
}
/**
* 从节点i开始进行调整
*
* @param d
* 要调整的数组
* @param i
* 从节点i开始
* @param n
* 数组的长度
*/
public static void heapMakeDown(int[] d, int i, int n) {
int j, tmp;
tmp = d[i];
j = 2 * i + 1;
while (j < n) {
if (j + 1 < n && d[j + 1] < d[j]) // 寻找左右孩子中小的那一个
j++;
if (tmp <= d[j])// 父节点的值比左右孩子中小的那个还小,则不需要调整
break;
d[i] = d[j];
i = j;
j = 2 * i + 1;
}
d[i] = tmp;
}
###归并排序
基本思想:归并排序用了分治的思想。将两个有序的序列,合并为一个序列。只需将两个序列的第一个值比较,将较小的元素添加到合并的序列,删除这个较小的元素,再继续比较。直到某一个序列为空,就可以将另一个序列的元素添加到合并的序列。
具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/**
* 合并d[first]-->d[mid],d[mid+1]-->d[last]
*
* @param d
* 要排序的数组
* @param first
* 起始下标
* @param mid
* 中间下标
* @param last
* 结束下标
* @param tmp
* 临时数组
*/
public static void merge(int[] d, int first, int mid, int last, int[] tmp) {
int i = first, j = mid + 1;
int index = 0;
while (i <= mid && j <= last) { // 从中选取小的那一个加入新的数组
if (d[i] < d[j]) {
tmp[index++] = d[i++];
} else {
tmp[index++] = d[j++];
}
}
// 加入d[first]-->d[mid],d[mid+1]-->d[last]中长度更长的数组的剩余元素
while (i <= mid) {
tmp[index++] = d[i++];
}
while (j <= last) {
tmp[index++] = d[j++];
}
for (i = 0; i < index; i++) {
d[first + i] = tmp[i];
}
}
/**
* 归并排序(递归)
*
* @param d
* 要排序的数组
* @param first
* 起始下标
* @param last
* 结束下标
* @param tmp
* 临时数组,用来存放排好序的元素
*/
public static void mergeSort(int[] d, int first, int last, int[] tmp) {
if (first < last) {
int mid = (first + last) / 2;
mergeSort(d, first, mid, tmp);
mergeSort(d, mid + 1, last, tmp);
merge(d, first, mid, last, tmp);
}
}
###快速排序
基本思想:快速排序使用了“分治法”。先从一个序列中找到一个基准元素,将序列分为两部分,左部分元素值都小于等于基准元素;右部分元素值都大于基准元素。递归的把左右两部分序列继续此操作,直至序列元素为1.
以下面一组数据为例:
{ 8, 9, 2, 5, 7, 10, 12, 16, 18, 20 }
具体过程:
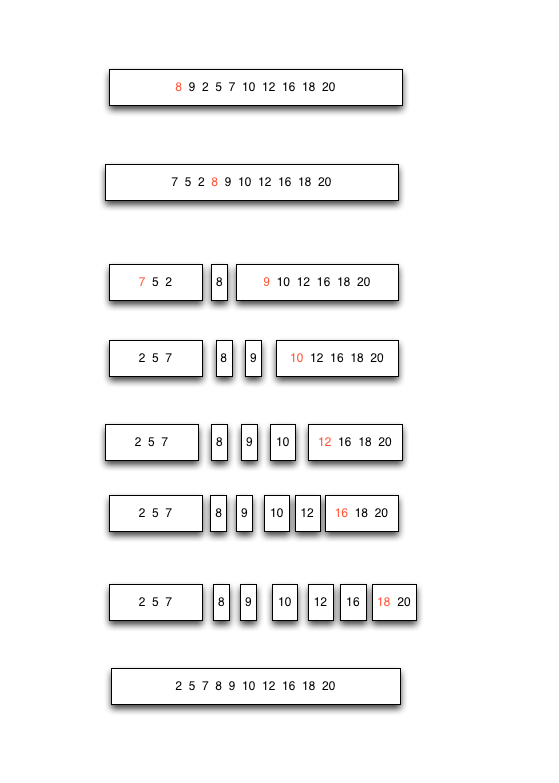
这一组数据也可以说明快速排序是不稳定的。在序列大多数都有序的情况下,选择快排不一定是最好的选择。
具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
* 快速排序
*
* @param d
* 要排序的数组
* @param first
* 开始下标
* @param last
* 结束下标
*/
public static void quickSort(int[] d, int first, int last) {
if (first >= last)
return;
int i = first, j = last;
int pivot = d[i];// 选取第一个元素作为基准元素
while (i < j) {
while (i < j && d[j] > pivot) { // 从右往左找比基准元素小的元素
j--;
}
if (i < j) {
d[i++] = d[j];
}
while (i < j && d[i] <= pivot) { // 从左往右找比基准元素大的元素
i++;
}
if (i < j) {
d[j--] = d[i];
}
}
d[i] = pivot;// 这时i = j,将基准元素放在这个位置
quickSort(d, first, i - 1);
quickSort(d, i + 1, last);
}
###选择排序
基本思想:选择排序就是将序列中未排序的部分中的最小元素,放入到序列的已排序部分的首位;接着在未排序部分继续寻找最小元素,放入已排序部分的末尾,直到所有元素排序完毕。 以下的每个排序中使用的数据都相同。
具体过程:
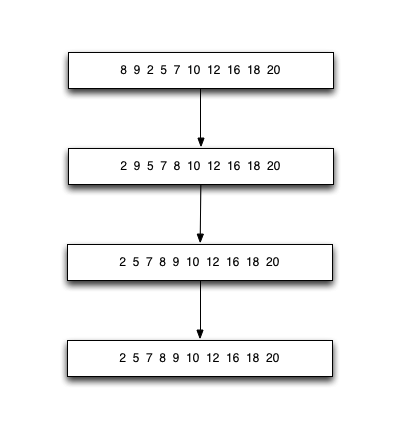
具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
* 选择排序
*
* @param d
* 要排序的数组
* @param n
* 数组的长度
*/
public static void selectSort(int[] d, int n) {
int tmp;
Boolean flag = false;
for (int i = 0; i < n - 1; i++) {
for (int j = i + 1; j < n; j++) { // 记住索引与直接交换的区别?
if (d[i] > d[j]) {
tmp = d[i];
d[i] = d[j];
d[j] = tmp;
flag = true;
}
flag = false;
}
if (flag)
break;
}
}
###插入排序
基本思想:插入排序是对每一个未排序元素,在已排序序列中从后往前查找,发现合适的位置将此元素插入到已排序序列,直到扫描完所有的未排序元素。
具体过程:
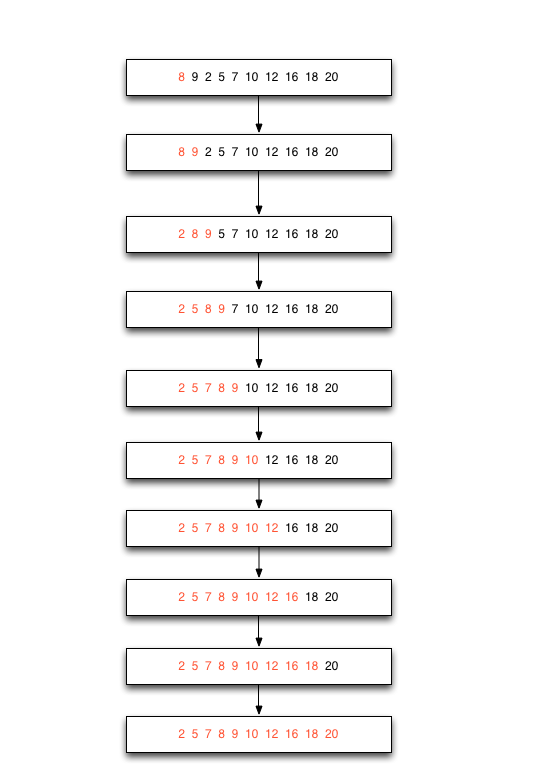
具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
* 插入排序
*
* @param d
* 要排序的数组
* @param n
* 数组的长度
*/
public static void insertionSort(int[] d, int n) {
int tmp;
for (int i = 1; i < n; i++) {
tmp = d[i];
int j = i - 1;
while (j >= 0 && d[j] > tmp) {
d[j + 1] = d[j];
j--;
}
d[j + 1] = tmp;
}
}
###冒泡排序
基本思想:比较相邻的两个元素,如果前一个元素比后一个元素大,则交换;记录下每次交换时的下标,下一次交换的时候仅需要从开始的元素到上轮交换的最后一个下标即可,优化了简单冒泡排序。
具体过程:
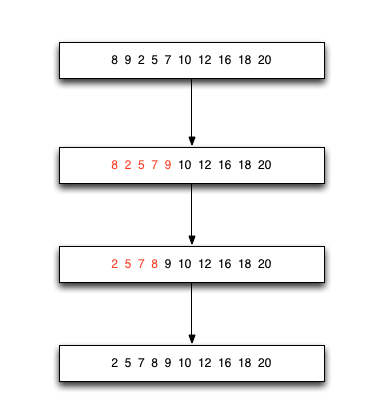
具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
* 冒泡排序
*
* @param d
* 要排序的数组
* @param n
* 数组长度
*/
public static void bubbleSort(int[] d, int n) {
int flag = n;
int j, tmp;
while (flag > 0) {
j = flag;
flag = 0;
for (int i = 1; i < j; i++) {
if (d[i] < d[i - 1]) {
tmp = d[i - 1];
d[i - 1] = d[i];
d[i] = tmp;
flag = i;// 记住有改变的下标,下一次只需要在0-->flag之间排序即可
}
}
}
}
